B-スプライン曲線

幾何学的性質

TrueTypeフォントの輪郭は2次のB-スプライン曲線で表現されます。

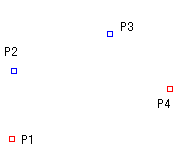
今、３点P1、P2、P3が与えられ、P1を開始点として、P2を曲線の制御点とし、P3を終点と仮定します。

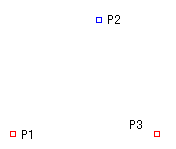
P1とP2、およびP2とP3を直線で結びます。

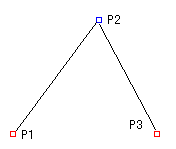
2つの直線を、２つに等分し、その中点をP4、P5とします。

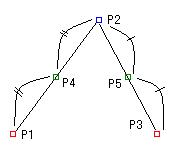
P4とP5を直線で結びます。

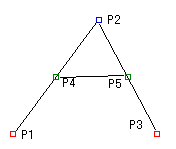
P4からP5へ引いた直線を２つに等分し、その中点をP6とします。

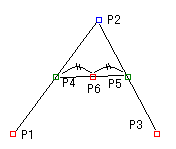
この時、2次のB-スプライン曲線は、点P6を通ります。

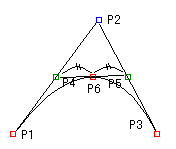
さらに、同様にして、P1からP4へ向かう直線を２つに等分し、P4からP6へ向かう直線も２つに等分し、その中点をそれぞれP7、P8とします。

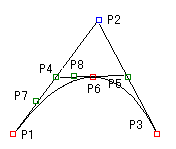
P7からP8へ引いた直線を２つに等分し、その中点をP9とします。2次のB-スプライン曲線は、点P9を通ります。

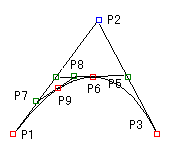
TrueTypeフォントの仕様書用語では、点P1やP3は「オンカーブ点」と呼ばれ、点P2は「オフカーブ点」と呼ばれます。

　

前の例では、オフカーブ点が１ヶでしたが、オフカーブ点が２ヶ連続する場合について説明します。

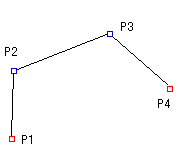
今、P1を開始点として、P2、P3をオフカーブ点とし、P4を終点と仮定します。

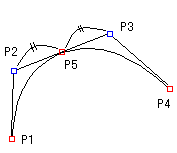
前と同様に、P1とP2、P2とP3、P3とP4を直線で結びます。

P2からP3へ引いた直線を２つに等分し、その中点をP5とします。2次のB-スプライン曲線は、点P5を通ります。

ちなみに、TTEditで円を描くと、

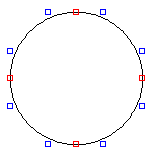
のようになりますが、厳密には円ではなくB-スプライン曲線で近似された円です。

上記の性質により、

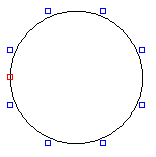
のようにオンカーブ点を省いても円になります。（開始点はオンカーブ点でなければならないので、少なくでも１つはオンカーブ点が含まれます。）

数学的表現

数式で2次B-スプライン曲線を表現すると、

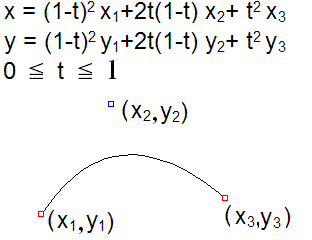
のようになります。

ここで、x１,y1はオンカーブ点、x2,y2はオフカーブ点、x3,y3はオンカーブ点です。

tは0から1までの値をとります。t=0の時、x=x1、y=y1になり、t=1の時、x=x3、y=y3になります。

仮に

x1=100、y1=100

ｘ2=200、y2=500

x3=400、y3=200

として、tを0.1ずつ大きくして計算してみます。

t=0.1の時

　x=(1-0.1)×(1-0.1)×100＋2×0.1×(1-0.1)×200＋0.1×0.1×400=121

　y=(1-0.1)×(1-0.1)×100＋2×0.1×(1-0.1)×500＋0.1×0.1×200=173

t=0.2の時

　x=(1-0.2)×(1-0.2)×100＋2×0.2×(1-0.2)×200＋0.2×0.2×400=144

　y=(1-0.2)×(1-0.2)×100＋2×0.2×(1-0.2)×500＋0.2×0.2×200=232

このようにして計算した結果を下の表にしめします。

t	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
x	100	121	144	169	196	225	256	289	324	361	400
y	100	173	232	277	308	325	328	317	292	253	200

tの増加量を0.1ではなく、0.01などにして計算し、xとyの関係をグラフに示すと、

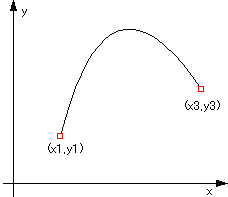
のようになります。

これが、2次B-スプライン曲線です。