3次のベジェ曲線

はじめに

PostScriptフォントや、PostsScript形式のOpenTypeフォントで採用されている曲線です。

OTEdit for WindowsやOTEdit for Macで使っている曲線となります。

幾何学的性質

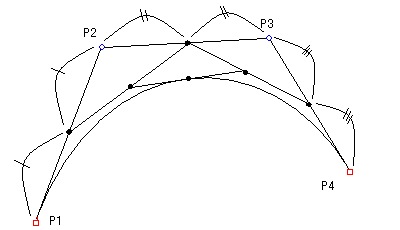
1つのベジェ曲線は、4つの制御点で構成され、両端の制御点は端点(アンカーポイント)、間の2点は方向点と呼ばれます。

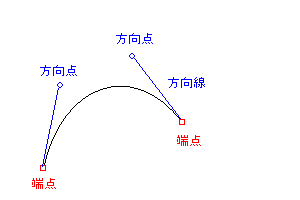
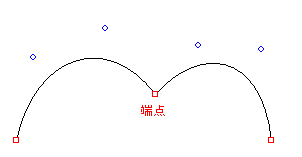
2つ以上のベジェ曲線がつながる場合は、手前のベジェ曲線の端点が、次のベジェ曲線の端点となります。

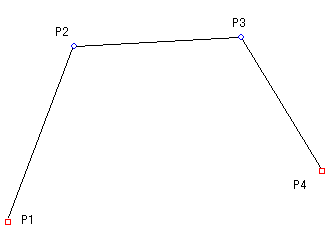
今、4点P1、P2、P3、P4が与えられ、P1、P4を端点、P2、P3を方向点とします。

P1とP2、P2とP3、P3とP4を直線で結びます。

それぞれの直線を2分割し、分割点を直線で結びます。

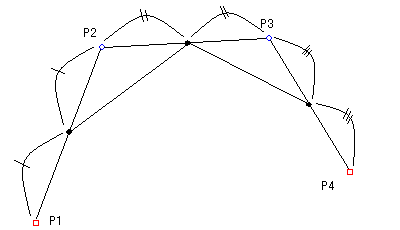
この分割を繰り返し、分割数を多くすれば、分割点はベジェ曲線となります。

数学的表現

数式で3次のベジェ曲線を表現すると、

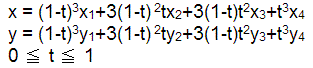
のようになります。

tは0から1までの値をとります。t=0の時、x=x1、y=y1になり、t=1の時、x=x4、y=y4になります。